
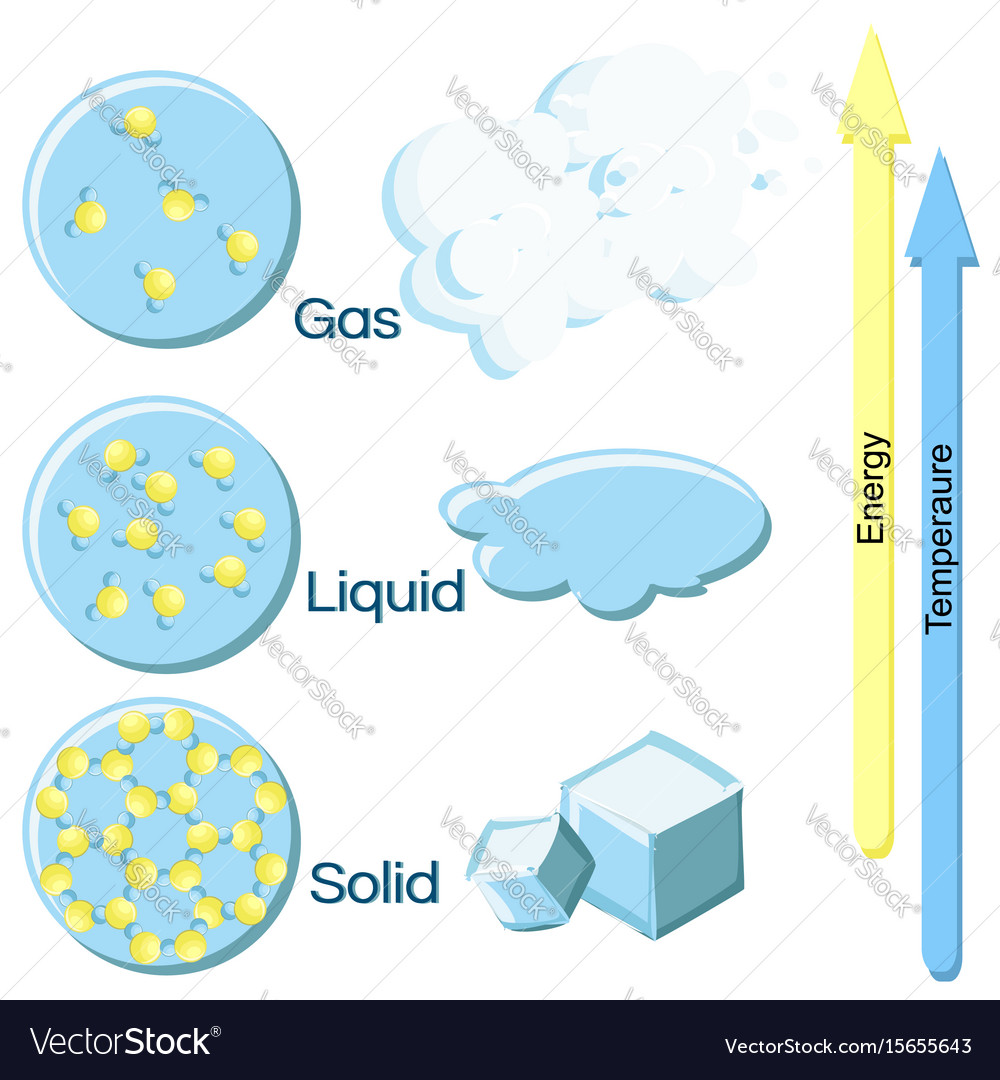
Helium, an atom made of two protons, two neutrons, and four electrons, is a stable atom made of an even number of fermions, and therefore behaves as a boson. You can place as many bosons in the ground-state configuration as you like, with no restrictions. If you create the right physical conditions - such as cooling a system of bosons and confining them to the same physical location - there is no limit to the number of bosons that you can fit into that lowest-energy state. When you reach this configuration, of many bosons all in the same, lowest-energy quantum state, you've achieved the fifth state of matter: a Bose-Einstein condensate. PoorLeno / Wikimedia Commonsīut this is not true for bosons. Because of the spin = 1/2 nature of the electron, only two (+1/2 and -1/2 states) electrons can be in any given state at once. The energy levels and electron wavefunctions that correspond to different states within a hydrogen. Any further electrons need to go into a progressively higher and higher energy state no two electrons can have the same exact quantum configuration in the same physical system.

To minimize the energy of its configuration, it drops into the same state, but needs to have its spin reversed: +½ if the first electron was -½ -½ if the first was +½. If you add a second electron, it will also try to get down to the ground state, but will find that it's already occupied.

The first electron will sink down to the lowest-energy configuration possible: the ground state. This comes into play when we start putting electrons onto a fully ionized atomic nucleus. It states that no two fermions can occupy the exact same quantum state as one another. The Pauli Exclusion Principle is one of the key cornerstones that was discovered in the early days of quantum mechanics. is only possible because of the Pauli exclusion rule that governs electrons, forbidding any two of them from occupying the same quantum state. The way that atoms link up to form molecules, including organic molecules and biological processes. Yes, their spins are different, but that difference leads to an amazing consequence: fermions obey the Pauli Exclusion Principle bosons do not. (Why? Because ±½ + ±½ can only equal -1, 0, or +1: the spin values for a boson.) Whether we're dealing with fundamental or composite particles, fermions and bosons exhibit a key difference from one another. However, if you bind a proton and a neutron together, you create a composite particle known as a deuteron: the atomic nucleus of a heavy isotope of hydrogen known as deuterium.Ī deuteron, which is a fermion bound together with another fermion, always behaves as a boson. Protons and neutrons, each of which are made up of three quarks apiece, also have spins that can only be ±½, as the spin of one quark will always oppose the spin of the other two. Siegel / Beyond The GalaxyĮlectrons, being fundamental particles with spins of ±½, are obviously fermions. are fundamental differences between fermionic particles and antiparticles and bosonic ones.
The particles and antiparticles of the Standard Model obey all sorts of conservation laws, but there.
Everything that we've ever measured behaves either as a fermion or a boson. In all the known Universe, there are no particles - fundamental or composite - that fall into any other category. This is a particle that, when we measure its spin, we always get values that are quantized in integer values of Planck's constant: 0, ☑, ☒, etc. This is a particle that, when we measure its spin (or intrinsic angular momentum), we always get values that are quantized in half-integer values of Planck's constant: ☑/2, ☓/2, ±5/2, etc. Here's the key point that will lead us to the fifth and sixth states of matter: every particle in the Universe, no matter whether it's a fundamental or a composite particle, falls into one of two categories. Individual protons, overall, behave as fermions, not as bosons.
STATE OF MATTER EXAMPLES FREE
The electrostatic repulsion and the attractive strong nuclear force, in tandem, are what give the proton its size, and the properties of quark mixing are required to explain the suite of free and composite particles in our Universe. antiquarks, and orbital angular momentum as well. The three valence quarks of a proton contribute to its spin, but so do the gluons, sea quarks and.


 0 kommentar(er)
0 kommentar(er)
